1. 첫번째 코드 - DFS

알고리즘 프로그래머스 P2

  • first.py의 문제점 (44점)
    1. DFS 는 복잡하다. BFS 사용하자 -> 해결 NO
    2. 33 + 33 는 해결하지 못한다 -> 해결 YES
# DFS 는 복잡하다. BFS 사용하자
def solution(N, number):
    array = [10] * 32001
    mark = [0] * 32001
    temp = [1,11,111,1111,11111]
    
    def dynamic(checkN, count, i):
        if not(0<checkN <32001) :
            return
        if count > 8 :
            return
        # if mark[checkN] == i:
        #    return
        if count > array[number]:
            return
    
        array[checkN] = count
        mark[checkN] = i

        if checkN == number:
            print(array[number], mark[checkN])
            return
        else:
            dynamic(checkN+N, count+1, i)
            dynamic(checkN-N, count+1, i)
            dynamic(checkN*N, count+1, i)
            dynamic(checkN//N, count+1, i)

    l = 5 if N < 3 else 4
    for i in range(1,l):
        start = temp[i-1] * N
        dynamic(start, i, i)
    
    answer = array[number] if array[number]  < 9 else -1
    return answer


if __name__ == "__main__":
    print(solution(5,12))

2. 두번쨰 코드 - DFS

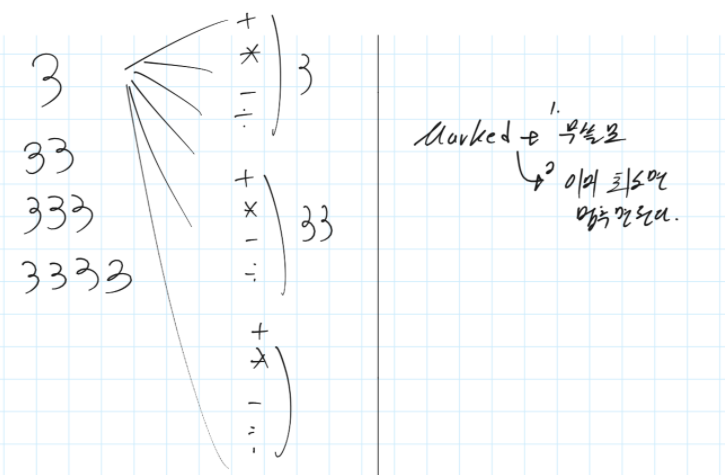
image

  • second.py의 문제점 (77점)
    1. 8을 return 해도 된는가 -> 7까지만 return 하도록 하면, 점수 떨어짐. 즉 8 return해야 함.
    2. 5, 26 = 55 + 5/5 로써 4가 답으로 나와야 함. But 나의 코드는 5가 나옴. ) "((55)+5)/5)"식으로 연산이 이뤄지기 떄문이다.
def solution(N, number):
    array = [10] * 32001
    esses = [N*i for i in [1,11,111,1111,11111] if N*i < 32001]  # good
    print(esses)
    
    def dynamic(checkN, count):
        if not(0<checkN <32001) :
            return
        if count > 8 :  # 8도 return 가능
            return
        if count > array[number]:
            return
    
        array[checkN] = count

        if checkN == number:
            return
        else:
            for j, nu in enumerate(esses):
                dynamic(checkN+nu, count+j+1)
                dynamic(checkN-nu, count+j+1)
                dynamic(checkN*nu, count+j+1)
                dynamic(checkN//nu, count+j+1)

    for i, num in enumerate(esses):     # good
        dynamic(num, i+1)
    
    answer = array[number] if array[number]  < 9 else -1    # 8도 return 가능
    return answer


if __name__ == "__main__":
    print(solution(5,26))

3. 세번쨰 코드 - Danamic programming

  • 정답 참조 링크는 게시물 맨 위에 있음.

  • Danamic programming 문제를 풀기 위해서는 재귀식을 세우는게 가장 중요하다.

  • 핵심 재귀식은 다음과 같다.

    N을 n번 사용해서 만들 수 있는 수 :
    N을 n번 연달아서 사용할 수 있는 수 U(합집합)
    N을 1번 사용했을 때 SET 과 n-1번 사용했을 때 SET을 사칙연산한 수들의 집합 U
    N을 2번 사용했을 때 SET 과 n-2번 사용했을 때 SET을 사칙연산한 수들의 집합 U
    ... U
    N을 n-1번 사용했을 때 SET 과 1번 사용했을 때 SET을 사칙연산한 수들의 집합

  • 나의 손코딩

  • 나의 코드
def solution(N, number):
    S = [0]
    for i in range(1,9):
        S.append({int(str(N)*i)})
    for i in range(1,9):
        for j in range(1,i):
            print(i,j,i-j)
            # set은 순서가 없기 때문에 list로 바꿔서 for해야하는 줄 알았는데 
            # 이런 방법으로 set내부의 모든 원소에 쉽게 접근할 수 있다. dict도 마찬가지 이다. 
            for num1 in S[j]: 
                for num2 in S[i-j]:
                    S[i].add(num1+num2)
                    S[i].add(num1-num2)
                    S[i].add(num1*num2)
                    if num2 != 0:
                        S[i].add(num1//num2)
        if number in S[i]:
            return i
    return -1



if __name__ == "__main__":
    print(solution(5,))

"""
위의 print로 나오는 수
2 1 1
3 1 2
3 2 1
4 1 3
4 2 2
4 3 1
5 1 4
5 2 3
5 3 2
5 4 1
6 1 5
6 2 4
6 3 3
6 4 2
6 5 1
7 1 6
7 2 5
7 3 4
7 4 3
7 5 2
7 6 1
8 1 7
8 2 6
8 3 5
8 4 4
8 5 3
8 6 2
8 7 1
"""

4. 참고하면 좋은 정답 코드

  • 참조 사이트는 맨 위에 기제.
  • 참조 사이트의 손 코딩도 읽으면 매우 좋으니 참조 할 것.
    def solution(N, number):
        # 허뎝님의 수정 피드백 -> 테스트 케이스가 바뀌면서 예외 사항을 추가해야 함.
        if N == number:
            return 1
            
        # 1. [ SET x 8 ] 초기화
        s = [ set() for x in range(8) ] 
        # 2. 각 set마다 기본 수 "N" * i 수 초기화
        for i,x in enumerate(s, start=1):
            x.add( int( str(N) * i ) )
        # 3. n 일반화
        #   { 
        #       "n" * i U 
        #       1번 set 사칙연산 n-1번 set U
        #       2번 set 사칙연산 n-2번 set U
        #       ...
        #       n-1번 set 사칙연산 1번 set, 
        #    } 
        # number를 가장 최소로 만드는 수 구함.
        for i in range(1, 8):
            for j in range(i):
                for op1 in s[j]:
                    for op2 in s[i-j-1]:
                        s[i].add(op1 + op2)
                        s[i].add(op1 - op2)
                        s[i].add(op1 * op2)
                        if op2 != 0:
                            s[i].add(op1 // op2)
            if  number in s[i]:
                answer = i + 1
                break
        else:
            answer = -1
        return answer