youtube 강의 링크 : 쓔튜브 선형대수 강의 링크

1강~5강까지는 매우 기초적인 내용이라 정리하지 않았습니다.

6강 Systems of linear equations

  1. 확장 행렬(Augmented matrix)이란? 선형연립방정식을 행렬로 표현한 것.

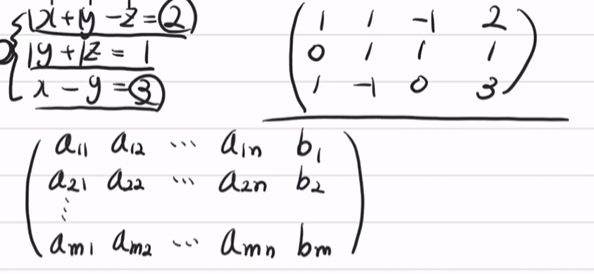
    image-20201111204926141

  2. reduced row echelon form (기약 행 사다리꼴)

    • 해가 이미 구해진 형태의 확장 행렬
    • x3 = 2라고 한다면 확장행렬의 한 row는 0 0 1 2가 될 것이다.
    • 아래의 4가지 규칙을 만족할 때 reduced row echelon form이라고 부를 수 있다.
      1. 영 행이 아니라면, 각 행에서 처음 등장하는 영이 아닌 수는 1이고, 이를 leading 1이라고 부른다.
      2. 영행은 항상 맨 아래에 모여있다.
      3. leading 1의 위치는 항상 한 칸 이상 뒤로 밀린다.
      4. leading 1이 포함된 열은 leading 1을 제외하면 모두 0이다.

Gauss Jordan Elimination (7강)

  • 일반적인 연립선형의 확장행렬을 reduced row echolon form(기약행사다리꼴)으로 바꿔주는 방법

    1. Elementary row operations(기본 행 연산)

      • 한 행에 상수배(=! 0) 하는 방법
      • 한 행의 상수배(=! 0)를 다른 행 더하기
      • 행 교환

    2. 가오스 소거법

      확장행렬을 기약 행 사다리꼴(row echelon = leading 1 아래로 0인 행렬)로 바꾸는 알고리즘

      • (1행부터 아래로) 기본 행 연산을 통해서 행 사다리꼴을 만들어 주는 과정
      • leading1 앞을 0으로 만들어주는 과정
      • 여기까지는 가오스 소거법이다.

    3. reduced (기약) 형태(leading1 뒤도 0인 행렬) 만들어 주기

      • 이게 가오스 조던 소거법이다.
      • (마지막행부터 위로 back substitution) 기본 행 연산을 통해서 기약(reduced) 행 사다리꼴을 만들어 주는 과정

  • 이 알고리즘을 통해서 컴퓨터로 해를 구하는 과정이 매우 쉬워졌다. 가감법 대입법을 사용해서 해를 구하면 엄청 오래 걸린다.

  • (8강 Gauss Jordan Elimination의 고찰) 가오스 조던 소거법은 왜 가능할까? 가오스 소거법이 연립 일차방정식의 가감법이다. 가오스 조던 소거법이 연립 일차방정식의 대입법이다.

행렬의 기본 연산과 이론

  • 13강 Identity matrix (항등행렬) - 행렬의 곱샘 항등원이다.

  • 14강 역행렬(inverse matrix, invertable (역행렬 존재하는 행렬=가역행렬))

    • 곱샘의 항등원에 대한 역원)
    • 귀류법을 이용한 증명에 의해, 한 행렬의 역행렬은 유일하다 (1개만 존재한다).
    • 영인자(zero divisor) - 0이 아닌 두 행렬을 곱해서 0이 나올 수 있다.
    • 가오스 조던 소거법을 이용한 역행렬 구하는 방법
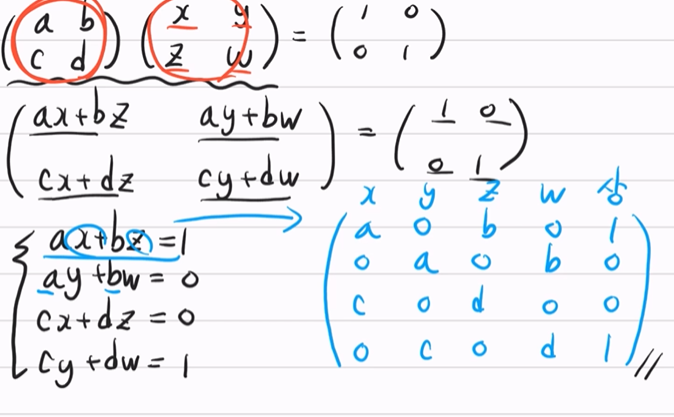
      • image-20201113213128976
      • 파랑색 행렬에 대해서, 가오스 조던 소거법을 사용해 x,y,z,w를 구하면 우리에게 익숙한 2차 정사각행렬의 역행렬 공식을 구할 수 있다.

  • 15강 역행렬의 성질

    • invertable (역행렬 존재하는 행렬=가역행렬)을 판단하는 방법? determinent(행렬식)=0 인지를 판단
    • non-invertible한 행렬? singular matrix. determinent(행렬식)=0인 metrix
    • 역행렬의 지수곱. 역행렬의 역행렬은 자기자신. 스칼라배는 역수.
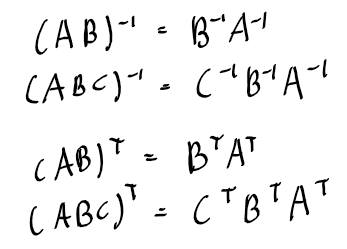
    • image-20201113222625212

  • 16강 전치행렬(transposed matrix)

    • 덧셈의 분배법칙 성립. (모든 증명은 동영상에 있다)
    • 곱셉의 분배법칙은 위와 같이 위치가 뒤바껴야 한다.
    • A가 invertable이면 transe(A)도 invertable이다.
    • inverse(trace(A)) = trace(inverse(A)) 이다.

  • 17강 대각합(trace)

    • n차 정사각행렬 A에 대해서, 대각성분들의 합을 대각합이라 한다.
    1. dot product와 행렬곱 사이의 관계
      • 열백터 -> 백터로 취급 가능하다.
      • dot product( • ) - 백터와 백터, 열백터와 열백터 (EX. (AB)ij => transe(Ai) • (Bj))
      • A : nxn, (n,v는 열백터) u : nx1, v : nx1 일때, Au • v = u • transe(A)v , u • Av = transe(A)u • v

기본 행렬과 가역행렬의 관계

  • 18강 기본행연산의 행렬화 (강의 꼭 한번 더 보기)

    • 열백터 -> 백터로 취급하기
      • 열백터의 행교환 = 백터의 좌표 뒤바꿈 -> 선형변환=선형사상(linear transformation) -> 이 변환식을 행렬로 표현(행렬화)할 수 있다.
        • 선형사상은 행렬로 표현할 수 있다.
        • 기본행 연산도 행렬로 표현할 수 있다.
      • y = f(x)의 함수로써 그 함수가 열백터의 행을 바꾸는 함수하면, 그 함수의 확장행렬은 아래와 같다.
      • image-20201113225645176
      • 즉 열백터의 행교환을 하고 싶으면 I의 행교환 시킨 행렬을 곱해주면 되고
      • 행렬 행백터의 열교환을 하고 싶으면 I의 열교환 시킨 행렬을 곱해주면 된다.
      • 스칼라곱을 하는 linear transformation으로, 한 행에 상수배를 해주고 싶으면, I의 i행에 상수배를 한 행렬이 변환행렬이다. (행렬화)
      • 이와 같은 **기본 행연산(행변환, 열변환, 상수배, 행or열이 일차 결합)**을 행렬화 할 수 있다. = 기본행렬

  • 19강 기본행렬(elementary matrix)과 기약행사다리꼴의 역행렬

    • 기본행렬 - 1. 행교환 2. 행의 상수배 3. 행의 상수배를 다른 행의 더하기. 이러한 역할을 하는 행렬을 의미한다. 이 3가지 역할 중 2개 이상을 수행하는 행렬은 기본행렬이라고 하지 않는다.(기본행렬 2개를 곱해주면 2개의 역할을 수행할 수 있긴 하지만. 그렇게 곱해서 나온 행렬은 기본행렬이라 하지 않는다.)
    • 기본행렬의 특징
      • n차 정사각행렬.
      • 선형사상이다(정의역과 치역의 Space가 동일하다. 다르거나 일부분이라면 선형사상이 아니다.) = 기본행렬은 항상 가역행렬이다. = 역행렬이 항상 존재 한다.
      • 항상 항등행렬을 이용해서 만든다(18강 처럼) = 그렇다면 그 행동과 완전히 반대대는 역할을 하는 행렬이 당연히 반드시 존재할 것이다. (ex, I의 i행과 j행을 행교환한 행렬 <-> I의 j행과 i행을 행교환한 행렬) 즉! 역행렬이 항상 존재한다.
    • 기약행사다리꼴 중 영행을 포함하는 행렬은 determinent=0 이다.(증명 나중에) 따라서 기약행사다리꼴 중 역행렬이 존재하는 행렬은 단위행렬 뿐이다.
    • 따라서! A가 가역행렬(역행렬이 존재하면)이면 A를 가오스 조던 소거법을 행하여 구한 기약행사다리꼴은 단위행렬이다!! = A에 가오스 조던 소거법을 적용하는 것이, **“기본행렬 연산을 여러번 수행”**하는 것이다. 따라서 A의 역행렬이 존재한다면, A에 가오스 조던 소거법을 취하면 단위행렬 형태가 되고, A의 역행렬은 위에서 적용한 **“기본행렬 연산의 여러번 수행”**이 역행렬 그 자체이다.

  • 20강 분할행렬과 역행렬 알고리즘

    • n차 정사각행렬 A에 대해서

    • 위의 명제의 역도 성립한다. A의 (가오스 조던 소거법을 적용해 구한) 기약행렬사다리꼴이 I라면, A는 가역행렬이다.

    • 이때 나오는 명제는 이것이다. A가 역행렬이 존재하면, A는 기본행렬들의 곱으로 표현가능하다.

    • 따라서 삼각형으로 연결된 3개의 명제는 서로서로 필요충분조건이다. 서로 동치(사실상 같은 말)이다.

    • image-20201115194429022

    • 행동치(row equivalent)를 이용한 A의 역행렬 구하기

      • Ek x … x E2 x E1 (기본 행 연산들) x A = B 에서 A와 B는 행동치이다.

        • = A에서 기본행 연산을 몇개 수행하면 B가 나온다
        • = B에서 기본행렬산을 몇개 수행하면 A가 나온다.

      • A와 I는 행동치이다.

        • = A에서 기본행 연산의 곱으로 표현가능하다.
        • = A는 가역이다.
        • 결론 : A와 I가 행동치이면, A를 항등행렬로 바꿔주는 “기본행 연산의 행렬들을” 그대로 항등행렬에 곱해주면, A의 역행렬이 나온다
        • A = Ek x … x E2 x E1 (기본 행 연산들) 일 때,
          • Ek x … x E2 x E1 (기본 행 연산들) x inverse(A) = I
          • I x inverse(A) = inverse( Ek x … x E2 x E1 (기본 행 연산들) ) x I 이므로, 아래와 같이 하면 된다.
        • 블록행렬(분할행렬) = A의 역행렬 구하기
          1. Ek x … x E2 x E1 (기본 행 연산들) = 가오스 조던 소거법을 위한 기본행 연산들
          2. 이 연산들을 I에다가도 적용해 주기
          3. 따로따로 계산하지 말고 블록으로 묶어서 한번에 연산하기
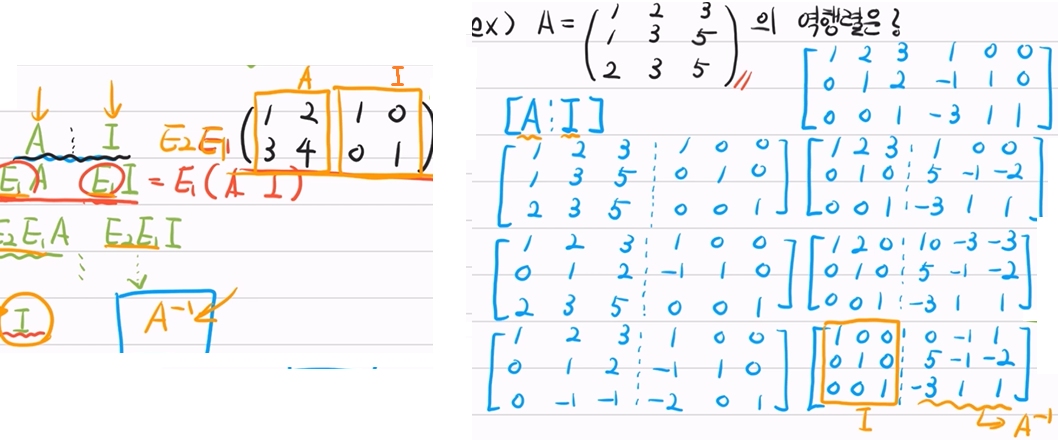
          4. image-20201120124739888

연립선형방정식과 행렬의 관계

  • 21강 연립선형방정식과 행렬의 관계1

    • A x = B (nxn) (nx1) (nx1)
    • consistent : 해가 적어도 한 개가 있는 경우
    • inconsistent : 해가 전혀 없는 경우
    • homogeneous : 동차 연립선형방정식 (B=0인 경우. A에 역행렬이 존재하면 자명해 만을 가진다.)

  • 22강 연립선형방정식과 행렬의 관계2

    • 선형함수/선형사상 - ‘선형적인 곱과 덧셈으로만 이루어진 식’ 말고 수학적 정의
      1. 가산성 f(x+y) = f(x) + f(y)
      2. 동차성 a * f(x) = a * f(x)
    • 행렬연산: A(x+y) = Ax+Ay , A(ax) = aAx -> 선형 사상이다!
    • 연립성형방정식과 역행렬과의 관계
      • A x = B (nxn) (nx1) (nx1)
      • A가 가역이면(b!=0), 방정식의 해는 존재하고 유일하다. (유일해를 가진다)
        • Y는 x의 유일해.
        • augmented matrix(A:b) --가오스조던소거법–> (I:Y)
        • (위에 참조) A와 I는 행동치이다 = A는 가역행렬이다.
    • AB가 가역행렬이면 A와 B도 각각 가역행렬이다. (증명은 22강 참조)
      • 내가 만든 명제 : AB가 가역행렬이면, AB를 기본행연산들의 곱으로 표현가능하다. 그 기본행 연산들을 나눠서 한쪽을 A, 다른 한쪽을 B라고 할 수 있을 것이다. A와 B 또한 기본행 연산들의 곱이므로, 가역행렬이다.